Hydrodynamik in festen Schwämmen (Druckverlust, Maldistribution)
- Ansprechperson:
- Förderung:
DFG (FOR583 TP1,T3)
1 Hintergrund
Als feste Schwämme werden hochporöse, offenzellige und daher allseitig durchströmbare Netzwerkstrukturen aus keramischen oder metallischen Basismaterialien bezeichnet. Aufgrund der hohen Porosität besitzen sie einen vergleichsweise niedrigen Druckverlust. Die große spezifische Oberfläche sowie die kontinuierliche feste Phase begünstigen den Wärmetransport. Mögliche technische Anwendungen für deren Einsatz sind z.B. hochselektive Reaktoren, Porenbrenner, Abgaskatalysatoren oder Solarturmkraftwerke. Zur Auslegung dieser Technologien sind verlässliche Modelle zur Beschreibung des hydrodynamischen Verhaltens notwendig. Kenngrößen sind u.a. die spezifische Oberfläche, der Druckverlust und die Maldistribution.
2 Forschungsarbeiten
2.1 Geometrische Kenngrößen
Zur Beschreibung der Schwammstrukturen ist die Kenntnis geometrischer Kenngrößen unab-dingbar. Auch werden diese verwendet, um experimentelle Daten zum Druckverlust, Wärme-übergang und der Wärmeleitung zu korrelieren. Wichtigste Kenngröße hierbei ist die spezifi-sche Oberfläche. Zu deren Bestimmung wurde eine Versuchsmethodik erarbeitet, die auf Computer- und Kernspintomographiemessungen basiert. Aus Strukturrekonstruktionen (vgl. Abbildung 1) kann mit Hilfe eines numerischen Algorithmus die spezifische Oberfläche als charakteristischer Wert jeden Schwammtyps bestimmt werden.
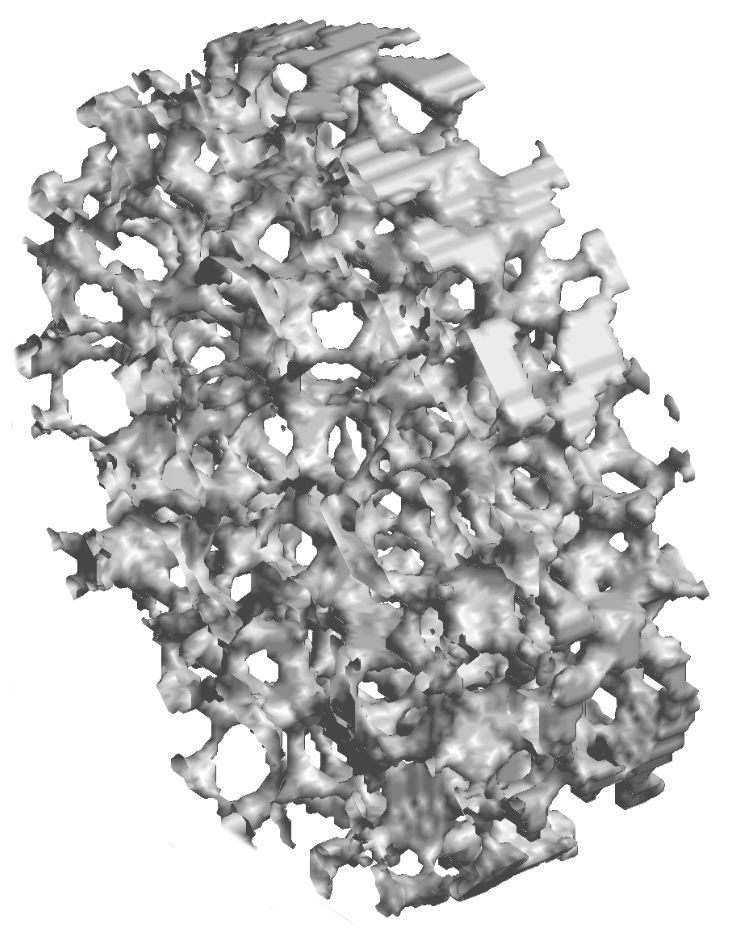

Abbildung 1: Rekonstruktion von Schwammstrukturen aus Kernspintomographiemessungen
2.1 Druckverlust
In Experimenten wurde für diverse Schwammtypen der Druckverlust ermittelt und Abhängig-keiten von der ppi-Zahl und der Porosität bestimmt. Die experimentellen Druckverlustdaten wurden mit Hilfe eines Ergun-ähnlichen Ansatzes (Polynom zweiten Grades) korreliert:
∆p/∆L=110⋅η/(ψ⋅dh2 )⋅u0+1,45⋅ρ/(ψ2⋅dh )⋅u02 mit dh=4⋅ψ/Sv
Ein Vergleich mit zahlreichen Literaturdaten zeigt eine sehr gute Übereinstimmung und die Anwendbarkeit der Korrelation für metallische und keramische Schwämme im Reynolds-Zahlen-Bereich zwischen 10-1 und 105 sowie für verschiedene den Schwamm durchströmende Fluide (Luft, Wasser, NaOH, Glyzerin). Abbildung 2 zeigt für verschiedene Metallschwämme die sehr gute Übereinstimmung von Literaturdaten mit der Korrelation.
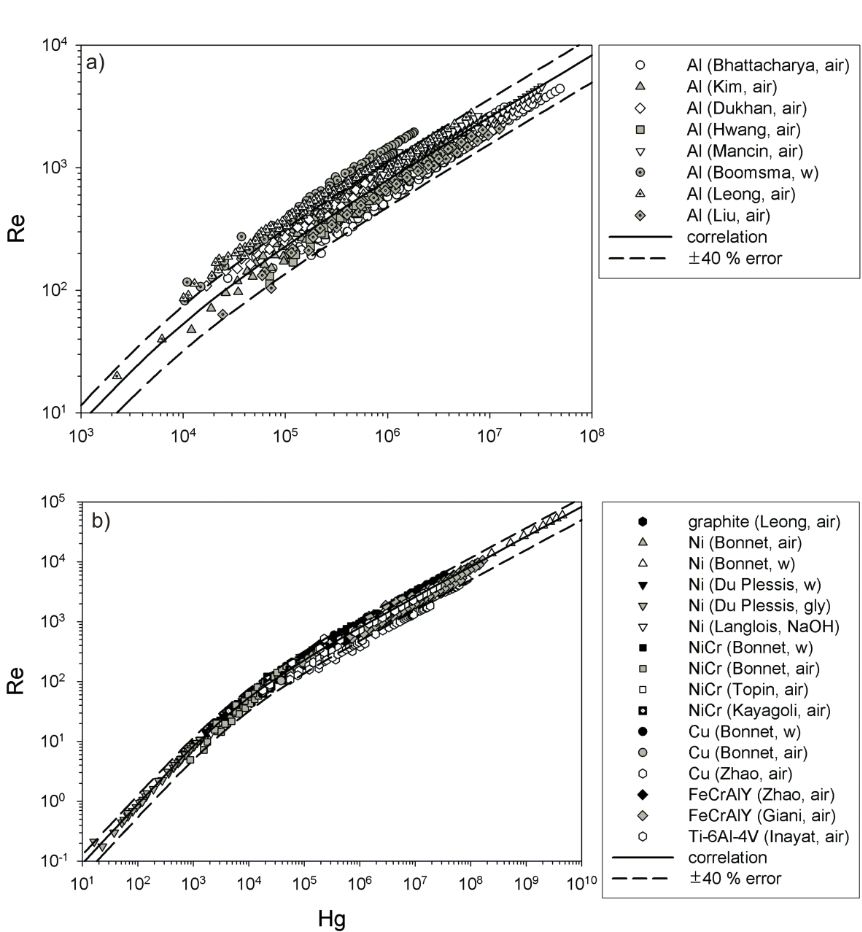
Abbildung 2: Impuls-Wärmetransport-Analogie für keramische Schwämme
2.3 Maldistribution
Mit Hilfe der bildgebenden Kernspintomographie wurde das Strömungsfeld verschiedener Schwammstrukturen bis zu einer Reynolds-Zahl von 125 untersucht (Fluid: Wasser). In Abbildung 3 ist die Mittelebene des Schwammes in Strömungsrichtung aus einem Experiment mit einem Al2O3-Schwamm (20 ppi, ψ=80%) dargestellt. Es ist eine deutliche Kanalisierung der Strömung und die Ausbildung von Totzonen zu erkennen. Es treten teilweise starke Geschwindigkeitsunterschiede auf. In weiteren Versuchen wurde mittels Röntgentomographie das hydrodynamische Verhalten bei der Durchströmung der Schwämme mit Gas-Wasser-Gemischen untersucht. Hier konnten u.a. Aufstaueffekte qualifiziert und quantifiziert werden.
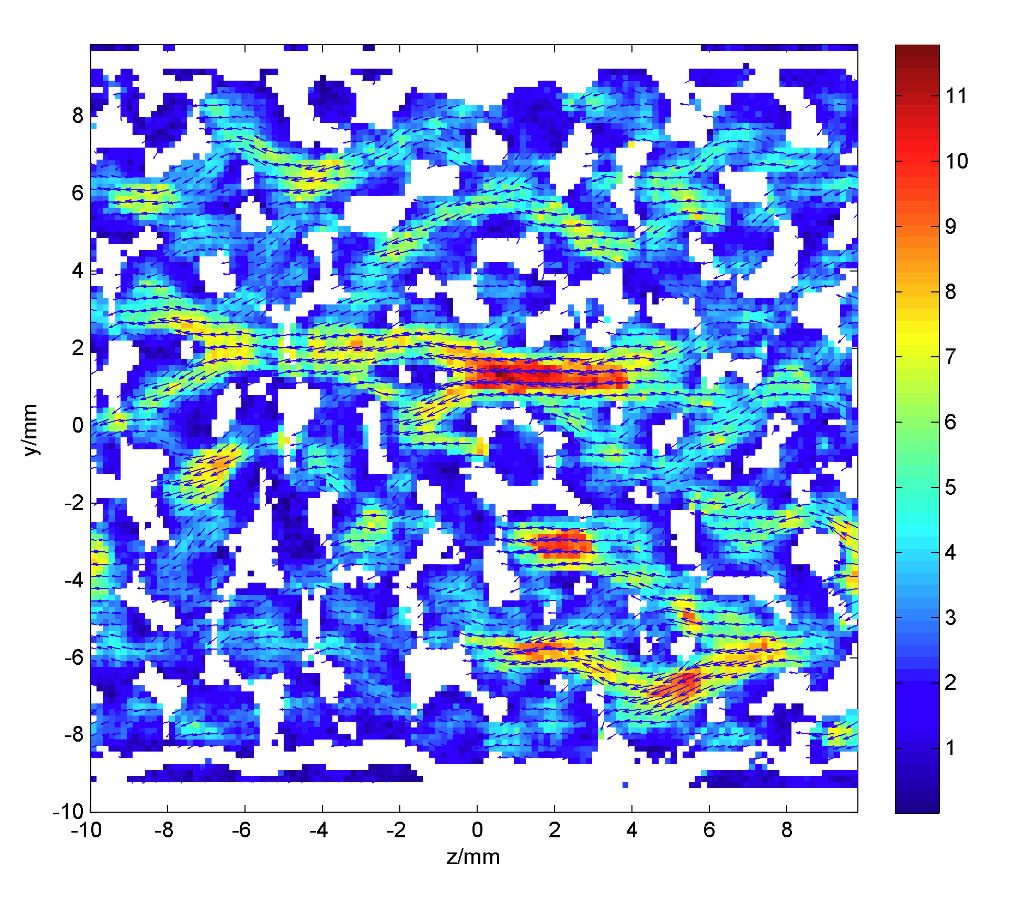
Abbildung 3: Strömungsfeld in einen Al2O3-Schwamm (20 ppi, ψ=80%), aufgenommen mit der bildgebenden Kernspintomographie, Re=125 , Fluid: Wasser
2.4 Veröffentlichungen
- B. Dietrich, W. Schabel, M. Kind, H. Martin, Pressure Drop Measurements of Ceramic Sponges – Determining the Hydraulic Diameter, Chemical Engineering Science 64 (16) (2009) 3633-3640.
- B. Dietrich, Pressure Drop Correlation for Ceramic and Metal Sponge, Chemical En-gineering Science 74 (1) (2012) 192-199.
- J. Große, B. Dietrich, H. Martin, M. Kind, J. Vicente, E. H. Hardy, Volume Image Analysis of Ceramic Sponges, Chemical Engineering & Technology, 31 (2) (2008) 307-314.
- J. Große, B. Dietrich, G. Garrido, P. Habisreuther, N. Zarzalis, H. Martin, M. Kind, B. Kraushaar-Czarnetzki. Morphological Characterisation of Ceramic Sponges for Appli-cations in Chemical Engineering. Industrial Engineering and Chemistry Research 48 (31), 2009, 10395-10401.

